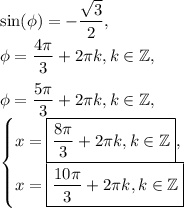Answer:
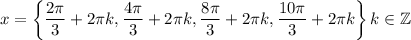
Explanation:
Hi there!
We want to solve for
 in:
in:
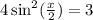
Since
 is in the argument of
is in the argument of
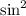 , let's first isolate
, let's first isolate
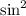 by dividing both sides by 4:
by dividing both sides by 4:
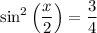
Next, recall that
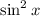 is just shorthand notation for
is just shorthand notation for
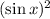 . Therefore, take the square root of both sides:
. Therefore, take the square root of both sides:
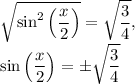
Simplify using
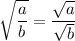 :
:
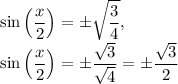
Let
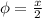 .
.
Case 1 (positive root):
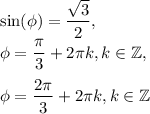
Therefore, we have:
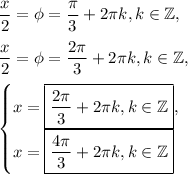
Case 2 (negative root):