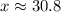Answer:
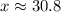
Explanation:
Note that the figure is a right triangle, and that we are given the length of the side adjacent to x and the hypotenuse of the triangle.
Therefore, we can use the cosine ratio. Recall that:
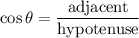
The adjacent side is 8.5 and the hypotenuse is 9.9. Therefore:
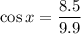
We can take the inverse cosine of both sides:
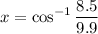
Use a calculator. Hence: