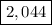Answer:
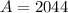
Explanation:
Note that
 denotes that
denotes that
 is a whole number.
is a whole number.
By definition, consecutive numbers follow each other when we count up (e.g. 1, 2, 3).
Let's consider our conditions:
- A, B, and C are consecutive whole numbers greater than 2,000
- A is a multiple of 4
- B is a multiple of 5
- C is a multiple of 6
Since B is a multiple of 5, the ones digit of B must be either 0 or 5. However, notice that the number before it, A, needs to be a multiple of 4. The ones digit of a number preceding a ones digit of 0 is 9. There are no multiples of 4 that have a ones digit of 9 and therefore the ones digit of B must be 5.
Because of this, we've identified that the ones digit of A, B, and C must be 4, 5, and 6 respectively.
We can continue making progress by trying to identify the smallest possible whole number greater than 2,000 with a units digit of 6 that is divisible by 6. Notice that:
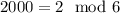
Therefore,
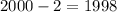 must be divisible by 6. To achieve a units digit of 6, we need to add a number with a units digit of 8 to 1,998 (since 8+8 has a units digit of 6).
must be divisible by 6. To achieve a units digit of 6, we need to add a number with a units digit of 8 to 1,998 (since 8+8 has a units digit of 6).
The smallest multiple of 6 that has a units digit of 8 is 18. Check to see if this works:
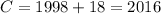
Following the conditions given in the problem, the following must be true:
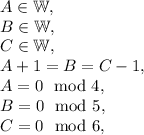
For
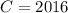 , we have
, we have
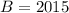 and
and
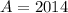 :
:

Not all conditions are met, hence this does not work. The next multiple of 6 that has a units digit of 8 is 48. Adding 48 to 1,998, we get
 .
.
For
 , we have
, we have
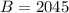 and
and
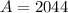 . Checking to see if this works:
. Checking to see if this works:
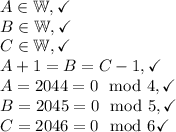
All conditions are met and therefore our answer is