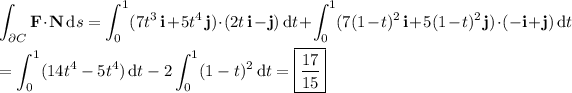Split up the boundary of C (which I denote ∂C throughout) into the parabolic segment from (1, 1) to (0, 0) (the part corresponding to y = x ²), and the line segment from (1, 1) to (0, 0) (the part of ∂C on the line y = x).
Parameterize these pieces respectively by
r(t) = x(t) i + y(t) j = t i + t ² j
and
s(t) = x(t) i + y(t) j = (1 - t ) i + (1 - t ) j
both with 0 ≤ t ≤ 1.
The circulation of F around ∂C is given by the line integral with respect to arc length,
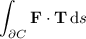
where T denotes the tangent vector to ∂C. Split up the integral over each piece of ∂C :
• on the parabolic segment, we have
T = dr/dt = i + 2t j
• on the line segment,
T = ds/dt = -i - j
Then the circulation is
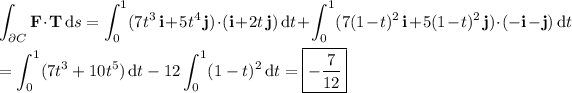
Alternatively, we can use Green's theorem to compute the circulation, as
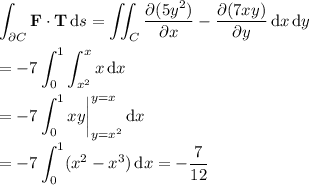
The flux of F across ∂C is
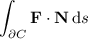
where N is the normal vector to ∂C. While T = x'(t) i + y'(t) j, the normal vector is N = y'(t) i - x'(t) j.
• on the parabolic segment,
N = 2t i - j
• on the line segment,
N = - i + j
So the flux is