Question

Please show detailed work if possible-that will help me to better understand the questions

start with this expression:
f(x) = 2x2 − x − 10

1st- What are the x-intercepts of the graph of f(x)? Show work on how to get this

2nd- Is the vertex of the graph of f(x) going to be a maximum or minimum? What are the coordinates of the vertex? Show work on how to get this

Part C: What are the steps you would use to graph f(x)? show how you can use the answers obtained in Part A and Part B to draw a graph

Answer 1

A chord of a circle is 9cm long if it's distance from the centre of the circle is 5cm calculate the radius of the circle

Answer 2

We are given the function:

`f(x)=2x^2-x-10`

`Here,\\a=2, b=-1,c=-10`

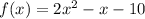
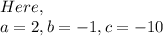
1. X-intercepts are the points at which the graph of a function intersects or cuts the x-axis. Since the x-intercept always lies on the x-axis, its ordinate or y-coordinate will always be 0. Since the function is quadratic, it will have at most 2 x-intercepts.

In order to find the x intercept, we basically solve for x at y=0:

`f(x)=2x^2-x-10\\As\ y=0,\\0=2x^2-x-10\\2x^2-x-10=0\\ 2x^2-5x+4x-10=0\\x(2x-5)+2(2x-5)=0\\(x+2)(2x-5)=0\\Hence,\\Individually:\\x=-2,\ x=(5)/(2)`

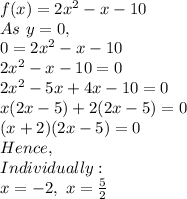
Hence, the x-intercepts of the parabola of f(x) is (-2,0),(2.5,0)

2. The vertex of parabola is determined as maximum or minimum, solely on how it opens. This depends on the nature of the co-efficient of the x^2 term or 'a'. If a is positive the parabola opens upwards (minimum point) and downwards (maximum point) if negative. Hence, here as a=2, the parabola opens upwards and its vertex is minimum.

`Vertex=((-b)/(2a),(-D)/(4a))\\Hence,\\D=b^2-4ac\\Substituting\ a=2,b=-1,c=-10:\\D=(-1)^2-4*2*-10=1+80=81\\Hence,\\Vertex\ of\ f(x)=((-(-1))/(2*2),(-81)/(4*2))=((1)/(4),(-81)/(8))`

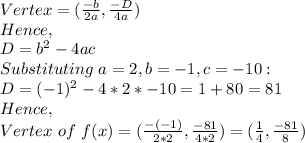
3. [Please refer to the attachment]

From the graph, we observe that the parabola cuts the x-axis at (-2,0),(2.5,0). Also, its clear that the axis of symmetry passes through
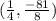`((1)/(4),(-81)/(8))`, which is its minimum point.