
Given :-
- Here, we have four exterior angles of the quadrilateral that is 9x° , 4x° , (5x - 10)° , (5x + 25)°
To Find :-
- We have to find the measurement of all the exterior angles
Let's Begin :-
Here, we have
- Angle ABD = 9x°
- Angle CDB = 4x°
- Angle HGE = (5x - 10)°
- Angle DEG = ( 5x + 25)°
We know that,
- Sum of interior angle and exterior angle is equal to 180°
Therefore,
Interior angles of the given quadrilateral
- Angle B= 180° - 9x°
- Angle D = 180° - 4x°
- Angle E = 180° - ( 5x + 25)°
- Angle G = 180° - ( 5x - 10)°
We also know that,
- The sum of angles of quadrilateral is 360°
That is,
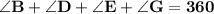
Subsitute the required values,
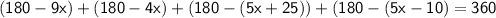
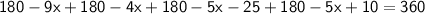
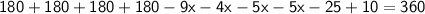
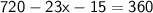
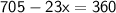

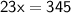
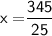


Thus, The value of x is 15°
Therefore,
All the exterior angles of the given quadrilateral are :-
Angle ABD
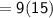
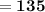
Angle CDB

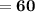
Angle HGE
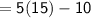
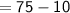

Angle DEG

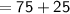
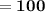
Hence, All the exterior angles of the given quadrilateral are 135° , 60° , 65° and 100°