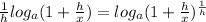Question

If f(x)=logx, show that f(x+h)-f(x)/h=log[1+h/x]^1/h, h=/=0 (Picture attached, thank you!)

Answer 1

Step by step proof shown below.

Explanation:

To prove the equation, you need to apply the Logarithm quotient rule and the Logarithm power rule. Here's how the quotient rule looks like.

`log_b(x/y) = log_b(x) - log_b(y)`

And here's how the power rule looks like

`log_a(x)^n = nlog_a(x)`

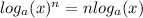
First let's apply the quotient rule.

`(f(x+h)-f(x))/(h) = (log_a(x+h)-log_a(x) )/(h) = (log_a((x+h)/(x) ))/(h)`

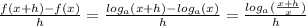
Now we can do some quick simplification, and apply the power rule.

`(1)/(h) log_a(1 + (h)/(x) ) = log_a(1+(h)/(x) )^(1)/(h)`