Question

A builder wants to fence in a rectangular space utilizing 80 feet of fencing. If the length is to be four feet more than twice that of the width, determine the dimensions of the rectangular space.

For this problem you must show the following:

a) A system of equations

b) Correct solve steps

c) Correct interpretation with correct units of measurement.

Answer 1

A)Let "L" represents lenght and "W" represent the width

L=2W+4

L+W=80

B) 1. W= 80-L

2. L=2(80-L)+4

3. L=160-2L+4

4. L=164-2L

5. 3L=164

6. L=
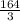`(164)/(3)` or 54.666

plug in 52 for L back into the original equation to solve W

7.
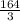`(164)/(3)` +W= 80

8. W=25.333 or
`(76)/(3)`

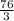
C) The widght is 25.33 feet and the lenght is 55.66 feet