Answer:
Step-by-step explanation:
Newton's Second Law is pretty much the standard for all motion that involves a force. It applies to gravitational force and torque and friction and weight on an elevator. The main formula for force is
F = ma. We have to adjust that to take into account that when the elevator is moving up, that "surge" of acceleration weighs down a bit on the scale, causing it to read higher than the actual weight until the acceleration evens out and there is no acceleration at all (no acceleration simply means that the velocity is constant; acceleration by definition is a change in velocity, and if there is no change in velocity, there is 0 acceleration). The force equation then becomes
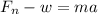 where
where
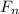 is normal force. This is what the scale will read, which is what we are looking for in this problem (our unknown). Since we are looking for
is normal force. This is what the scale will read, which is what we are looking for in this problem (our unknown). Since we are looking for
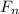 , that is what we will solve this literal equation for:
, that is what we will solve this literal equation for:
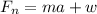 . m is the mass of the boy, a is the acceleration of the elevator (which is going up so we will call that acceleration positive), and w is weight. We have everything but the unknown and the weight of the boy. We find the weight:
. m is the mass of the boy, a is the acceleration of the elevator (which is going up so we will call that acceleration positive), and w is weight. We have everything but the unknown and the weight of the boy. We find the weight:
w = mg so
w = 28(9.8) and
w = 274.4 N BUT rounding to the correct number of significance we have that the weight is actually
w = 270 N.
Filling in the elevator equation:
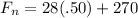 and according to the rules of significant digits, we have to multiply the 28(.50) {notice that I did add a 0 there for greater significance; if not that added 0 we are only looking at 1 significant digit which is pretty much useless}, round that to 2 sig fig's, and then add to 170:
and according to the rules of significant digits, we have to multiply the 28(.50) {notice that I did add a 0 there for greater significance; if not that added 0 we are only looking at 1 significant digit which is pretty much useless}, round that to 2 sig fig's, and then add to 170:
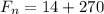 and adding, by the rules, requires that we round to the tens place to get, finally:
and adding, by the rules, requires that we round to the tens place to get, finally:
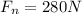 So you see that the surge in acceleration did in fact add a tiny bit to the weight read by the scale; conversely, if he were to have moved down at that same rate, the scale would have read a bit less than his actual weight). Isn't physics like the coolest thing ever!?
So you see that the surge in acceleration did in fact add a tiny bit to the weight read by the scale; conversely, if he were to have moved down at that same rate, the scale would have read a bit less than his actual weight). Isn't physics like the coolest thing ever!?