Answer:
The absolute maximum is about -5.84 at x = -2.
And the absolute minimum is about -11.28 at x = -π/6.
Explanation:
We want to find the absolute maximum and minimum values of the function:
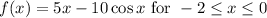
First, we should evaluate the endpoints of the interval:
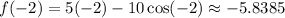
And:
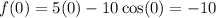
Recall that extrema of a function occurs at its critical points. The critical points of a function are whenever its derivative is zero or undefined.
So, find the derivative of the function:
![\displaystyle f'(x) = (d)/(dx)\left[ 5x - 10\cos x\right]](https://img.qammunity.org/2022/formulas/mathematics/college/dbwwn3bdij7l5za4w7qlfa97htp8mq2wiw.png)
Differentiate:

Set the function equal to zero:
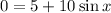
And solve for x:
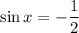
Using the unit circle, our solutions are:
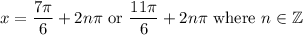
There is only one solution in the interval [-2, 0]:

Thus, we only have one critical point on the interval.
Substituting this back into the function yields:

In conclusion, the absolute maximum value of f on the interval [-2, 0] is about -5.8385 at x = -2 and the absolute minimum value of f is about -11.2782 at x = -π/6.
We can see this from the graph below as well.