Answers: x = 1 and x = 9
============================================================
Step-by-step explanation:
We'll use the distance formula here. Rather than compute the distance d based on two points given, we'll go in reverse to use the given distance d to find what the coordinate must be to satisfy the conditions.
We're given that d = 5
The first point is
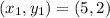 and the second point has coordinates of
and the second point has coordinates of
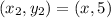 where x is some real number.
where x is some real number.
We'll plug all this into the distance formula and solve for x.
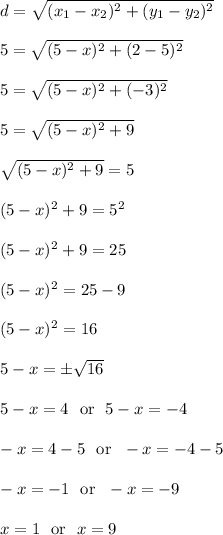
This means that if we had these three points
- A = (5, 2)
- B = (1, 5)
- C = (9, 5)
Then segments AB and AC are each 5 units long.