Question

A car has a mass of 2000 kg. While it is traveling along a perfectly flat road, it goes around an unbanked turn that has a radius of 40.0 m. The coefficient of static friction between the car tires and the road is 0.500. The car travels successfully around the turn at a constant speed of 10.0 m/s. Calculate the magnitude of the car's acceleration as it goes around the turn. _______ m/s^2

Answer 1

2.5 m/s²

Step-by-step explanation:

The given parameters are;

The mass of the car, m = 2,000 kg

The radius of the car, r = 40.0 m

The coefficient of friction between the car tires and the road, μ = 0.500

The constant speed with which the car moves, v = 10.0 m/s

The normal reaction of the road on the car, N = The weight of the car;

∴ N = m × g

Where;

g = The acceleration due to gravity ≈ 9.81 m/s²

N ≈ 2,000 kg × 9.81 m/s² = 19,620 N

The frictional force,
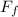`F_f` = μ × N

The centripetal force,
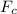`F_c` = m·v²/r

The car moves without slipping when
`F_f` =
`F_c`

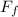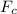
Therefore,
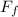`F_f` = 0.500 × 19,620 N = 2,000 kg ×
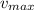`v_(max)`²/40.0 m

∴
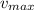`v_(max)` = √(0.500 × 19,620 N × 40.0 m/2,000 kg) ≈ 14.007 m/s

Therefore, the velocity with which the car moves, v <
`v_(max)`

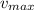
The cars centripetal acceleration,
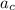`a_c` = v²/r

∴
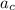`a_c` = (10.0 m/s)²/40.0 m = 2.5 m/s²

The cars centripetal acceleration as it goes round the turn,
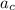`a_c` = 2.5 m/s².