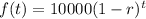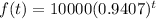Answer:
The function to determine the value of your car (in dollars) in terms of the number of years t since 2012 is:
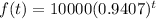
Explanation:
Value of the car:
Constant rate of change, so the value of the car in t years after 2012 is given by:
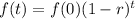
In which f(0) is the initial value and r is the decay rate, as a decimal.
In 2012 your car was worth $10,000.
This means that
 , thus:
, thus:
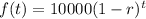
2014 your car was worth $8,850.
2014 - 2012 = 2, so:
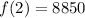
We use this to find 1 - r.
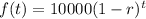
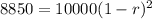
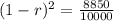
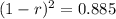
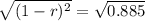
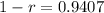
Thus