Question

A cylindrical vase has a diameter of 4 inches. At the bottom of the vase, there are 6 marbles, each of diameter 3 inches. The vase is filled with water up to a height of 8 inches. Which of the following could be used to calculate the volume of water in the vase?

π(2in)^2(8in) − 6(four over threeπ(1.5in)^3)
π(8in)^2(2in) − 6(four over threeπ(1.5in)^3)
π(2in)^2(8in) − 1.5(four over threeπ(6in)^3)
π(8in)^2(2in) − 1.5(four over threeπ(6in)^3)

Answer 1

The expression
`V = \pi \cdot (2\,in)^(2)\cdot (8\,in) -6\cdot \left[(4\pi)/(3)\cdot (1.5\,in)^(3) \right]` can be used to calculate the volume of water in the vase.

As vase is of cylindrical form and the six marbles are spherical, we shall derived an expression from volume formulas respective to Cylinder and Spheres. Firstly, we know that volume of water in the vase is equal to the Volume of the vase minus the volume occupied by the six marbles, that is to say:

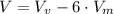`V = V_(v)-6\cdot V_(m)` (1)

Where:

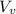`V_(v)` - Volume of the vase, in cubic inches.

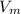`V_(m)` - Volume of the marble, in cubic inches.

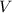`V` - Volume of water in the vase, in cubic inches.

Then, we expand (1) by volume formulas for the cylinder and sphere:

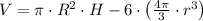`V = \pi\cdot R^(2)\cdot H - 6\cdot \left((4\pi)/(3) \cdot r^(3) \right)` (2)

Where:

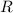`R` - Radius of the vase, in inches.

`H` - Height of the vase, in inches.

`r` - Radius of the marble, in inches.

If we know that
`R = 2\,in`,
`H = 8\,in`,
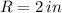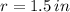`r = 1.5\,in`, then the following expression can be used to calculate the volume of water in the base:

`V = \pi \cdot (2\,in)^(2)\cdot (8\,in) -6\cdot \left[(4\pi)/(3)\cdot (1.5\,in)^(3) \right]`

In a nutshell, the expression
`V = \pi \cdot (2\,in)^(2)\cdot (8\,in) -6\cdot \left[(4\pi)/(3)\cdot (1.5\,in)^(3) \right]` can be used to calculate the volume of water in the vase.

Answer 2

The volume of the water is:
`\pi (2)^2(8) - 6 ((4)/(3) \pi (1.5)^3)`

The volume of a cylinder is;

`V = \pi r^2h`

For the cylinder, we have:

`d = 4` -- diameter

`h = 8` --- height of the water in the cylinder

The radius of the cylinder is:

`r =d/2 = 4/2 = 2`

So, the volume is:

`V = \pi * 2^2 * 8`

`V = \pi * (2)^2 (8)`

For the 6 marbles, we have:

`d = 3` --- the diameter of each

The shape of the marble is a sphere. So, the volume of 1 marble is:

`V = (4)/(3)\pi r^3`

The radius of 1 marble is:

`r = d/2 = 3/2 = 1.5`

So, the volume of 1 marble is:

`V_1 = (4)/(3) * \pi * (1.5)^3`

Multiply both sides by 6 to get the volume of the 6 marbles

`6 * V_1 = 6 * (4)/(3) * \pi * (1.5)^3`

`6V_1 = 6 * (4)/(3) * \pi * (1.5)^3`

`6V_1 = 6 ((4)/(3) \pi (1.5)^3)`

Recall that the volume of the cylinder is:

`V = \pi * (2)^2 (8)`

The volume of the water in the marble is the difference between the volume of the cylinder and the volume of the 6 marbles

So, we have:

`Volume = \pi (2)^2(8) - 6 ((4)/(3) \pi (1.5)^3)`