The dimension of a/b where x is the distance and t is the time is T
Given the expression
x = at + bt²
where
x is the distance
t is the time
Based on the homogeneity principle, the expression on the left-hand side must be equal to that on the right. Hence;
x = at
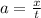
Since x is the distance and distance is measured in metres, the dimension equivalent will be the length 'L'
Since t is the time and time is measured in seconds, the dimension equivalent will be the seconds 'T'
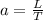
Similarly;
x = bt²
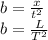
Next is to get a/b;
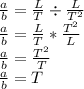
Hence the dimension of a/b is T