Answer:
1540
Explanation:
To figure out the answer you must compute 22 choose 3. To compute this, we can plug the values into the Combination formula, which goes like this:
 , where n is the sample size, and r is the amount being chosen. In this case, n is equal to the total 22 players, and r is the 3 players being chosen to fill the bottles. Plugging the values in, we have the answer as
, where n is the sample size, and r is the amount being chosen. In this case, n is equal to the total 22 players, and r is the 3 players being chosen to fill the bottles. Plugging the values in, we have the answer as
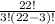 . 22 minus 3 simplifies to 19 factorial, and we can expand 22 factorial out from the numerator.
. 22 minus 3 simplifies to 19 factorial, and we can expand 22 factorial out from the numerator.
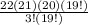
We can get rid of the 19 factorial from both the numerator and the denominator, and we are left with
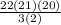
We can cancel out the 3 with the 3 in 21, and we can cancel out the 2 with the 2 in 20. We are left with
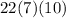
7 times 10 is equal to 70, and 70 times 22 is equal to 1540 total combinations.