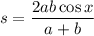Question

Find formula of s in terms of a, b, cos(x)

Answer 1

`\displaystyle s = (2ab\cos x)/(a+b)`

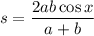
Explanation:

We want to find a formula for s in terms of a, b, and cos(x).

Let the point where s intersects AB be D.

Notice that s bisects ∠C. Then by the Angle Bisector Theorem:

`\displaystyle (a)/(BD) = (b)/(AD)`

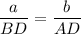
We can find BD using the Law of Cosines:

`\displaystyle BD^2 = a^2 + s^2 - 2as \cos x`

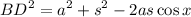
Likewise:

`\displaystyle AD^2 = b^2+ s^2 - 2bs \cos x`

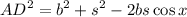
From the first equation, cross-multiply:

`bBD = a AD`

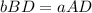
And square both sides:

`b^2 BD^2 =a^2 AD^2`

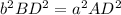
Substitute:

`\displaystyle b^2 \left(a^2 + s^2 - 2as \cos x\right) = a^2 \left(b^2 + s^2 - 2bs \cos x\right)`

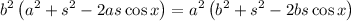
Distribute:

`a^2b^2 + b^2s^2 - 2ab^2 s\cos x = a^2b^2 + a^2s^2 - 2a^2 bs\cos x`

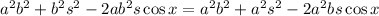
Simplify:

`b^2 s^2 - 2ab^2 s \cos x = a^2 s^2 - 2a^2 b s \cos x`

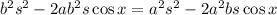
Divide both sides by s (s ≠ 0):

`b^2 s -2ab^2 \cos x = a^2 s - 2a^2 b \cos x`

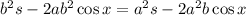
Isolate s:

`b^2 s - a^2s = -2a^2 b \cos x + 2ab^2 \cos x`

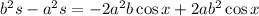
Factor:

`\displaystyle s (b^2 - a^2) = 2ab^2 \cos x - 2a^2 b \cos x`

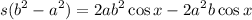
Therefore:

`\displaystyle s = (2ab^2 \cos x - 2a^2 b \cos x)/(b^2- a^2)`

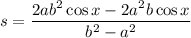
Factor:

`\displaystyle s = (2ab\cos x(b - a))/((b-a)(b+a))`

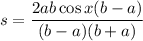
Simplify. Therefore:

`\displaystyle s = (2ab\cos x)/(a+b)`