Question

Use the Unit Circle to find the exact value of the trig function. Cos(45)

1/2
√2/2
√3/-2
1

Answer 1

In a unit circle a line reaching from origin to the circle's circumference specifies the trigonometric functions.

A point where the line which comes from origin to the circumference intersecting it has coordinates
`(\cos\theta,\sin\theta)`.

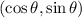In our case
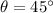`\theta=45^\circ` which lifts the line up by 45 degrees and makes it intersect circumference at
`(\cos45^\circ,\sin45^\circ)`.

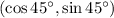In the upper right quadrant the angle between x and y axis is 90 degrees so a line coming in at angle of 45 degrees would split the quadrant in half, that means sine and cosine 45 degrees will be equal.

As you may noticed a point has coordinates cos, sin which means the distance between 0 and y coordinate where the point on a circle is, is called
`\cos\theta=\cos45^\circ`.

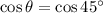Because cosine 45 degrees is so simple in interpretation it has a known value of
`\cos45^\circ=\sin45^\circ=(√(2))/(2)`.

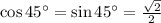Hope this helps :)