Question

In a clinical trial of a certain​ drug, 17 subjects experience headaches among the 221 subjects treated with the drug. Construct a ​95% ​(Wald) confidence interval estimate for the proportion of treated subjects who experience​ headaches.

a. Find the best point estimate of the population proportion.
b. Identify the value of the margin of error E.
c. Construct the confidence interval.
d. write a statement that correctly interprets the confidence interval.

Answer 1

Given :

n = 221

x = 17

a).
`$p=(17)/(221)$`

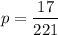
= 0.076

b). At the 95 confidence interval

Value of z = 1.96

Margin of error

`$=1.96 * \sqrt{(p(1-p))/(n)}$`

`$=1.96 * \sqrt{(0.076(1-0.076))/(221)}$`

`$=1.96 * \sqrt{(0.076* 0.924 )/(221)}$`

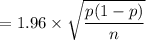
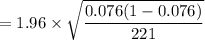
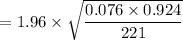
= 1.96 x 0.017

= 0.03332

c). confidence interval

= ( 0.076-0.033, 0.076+0.033)

= ( 0.043, 0.109 )

d). The confidence interval does not contain null value, so it is significant.