Answer:
The total distance, side to side, that the top of the building moves during such an oscillation is approximately 0.291 meters.
Step-by-step explanation:
Let suppose that the building is experimenting a Simple Harmonic Motion due to the action of wind. First, we determine the angular frequency of the system (
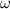 ), in radians per second:
), in radians per second:
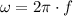 (1)
(1)
Where
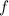 is the frequency, in hertz.
is the frequency, in hertz.
If we know that
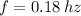 , then the angular frequency of the system is:
, then the angular frequency of the system is:
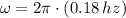

The maximum acceleration experimented by the system is represented by the following formula, of which we estimate amplitude of the oscillation:
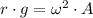 (2)
(2)
Where:
 - Ratio of real acceleration to free-fall acceleration, no unit.
- Ratio of real acceleration to free-fall acceleration, no unit.
 - Free-fall acceleration, in meters per square second.
- Free-fall acceleration, in meters per square second.
 - Amplitude, in meters.
- Amplitude, in meters.
If we know that
 ,
,
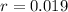 and
and
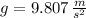 , then the amplitude of the oscillation is:
, then the amplitude of the oscillation is:
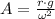
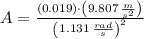
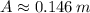
The total distance, side to side, is twice the amplitude, that is to say, a value of approximately 0.291 meters.