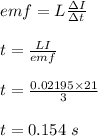Question

Calculate the self-inductance (in mH) of a 45.0 cm long, 10.0 cm diameter solenoid having 1000 loops. mH (b) How much energy (in J) is stored in this inductor when 21.0 A of current flows through it? J (c) How fast (in s) can it be turned off if the induced emf cannot exceed 3.00 V? s

Answer 1

(a) The self inductance, L = 21.95 mH

(b) The energy stored, E = 4.84 J

(c) the time, t = 0.154 s

Step-by-step explanation:

(a) Self inductance is calculated as;

`L = (N^2 \mu_0 A)/(l)`

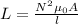
where;

N is the number of turns = 1000 loops

μ is the permeability of free space = 4π x 10⁻⁷ H/m

l is the length of the inductor, = 45 cm = 0.45 m

A is the area of the inductor (given diameter = 10 cm = 0.1 m)

`A = \pi r^2 = (\pi d^2)/(4) = (\pi * (0.1)^2)/(4) = 0.00786 \ m^2`

`L = ((1000)^2 * (4\pi * 10^(-7)) * (0.00786))/(0.45) \\\\L = 0.02195 \ H\\\\L = 21.95 \ mH`

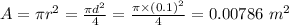
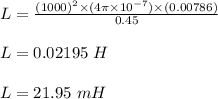
(b) The energy stored in the inductor when 21 A current ;

`E = (1)/(2)LI^2\\\\E = (1)/(2) * (0.02195) * (21) ^2\\\\E = 4.84 \ J`

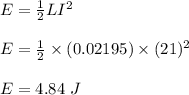
(c) time it can be turned off if the induced emf cannot exceed 3.0 V;

`emf = L (\Delta I)/(\Delta t) \\\\t = (LI)/(emf) \\\\t = (0.02195 * 21)/(3) \\\\t = 0.154 \ s`