Question

1. Paulina wants to find the width, AB, of a river. She walks along the edge of the river 200 ft and marks point C. Then she walks 60 ft further and marks point D. She turns 90° and walks until her location, point A, and point C are collinear. She marks point E at this location, as shown. (a) Can Paulina conclude that ΔABC and ΔEDC are similar? Why or why not? (b) Suppose DE = 40 ft. Calculate the width of the river, AB. Show all your work and round answer to the nearest tenth. Answer

Answer 1

Explanation:

a). In ΔABC and ΔEDC,

Since, AB and DE are parallel and AE is a transversal,

Therefore, ∠CAB ≅ ∠CED [Alternate interior angles]

m∠D = m∠B = 90°

ΔABC ~ ΔEDC [By AA property of similarity of two triangles]

b). Therefore, by the property of similar triangles,

"Corresponding sides of two similar triangles are proportional"

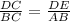
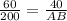
`(DC)/(BC)= (DE)/(AB)`

`(60)/(200)=(40)/(AB)`

AB =
`(40* 200)/(60)`

= 133.33

≈ 133.3 ft