Part (a)
Consecutive odd integers are integers that odd and they follow one right after another. If x is odd, then x+2 is the next odd integer
For example, if x = 7, then x+2 = 9 is right after.
Answer: x+2
========================================================
Part (b)
The consecutive odd integers we're dealing with are x and x+2.
Their squares are x^2 and (x+2)^2, and these squares add to 394.
Answer: x^2 + (x+2)^2 = 394
========================================================
Part (c)
We'll solve the equation we just set up.
x^2 + (x+2)^2 = 394
x^2 + x^2 + 4x + 4 = 394
2x^2+4x+4-394 = 0
2x^2+4x-390 = 0
2(x^2 + 2x - 195) = 0
x^2 + 2x - 195 = 0
You could factor this, but the quadratic formula avoids trial and error.
Use a = 1, b = 2, c = -195 in the quadratic formula.
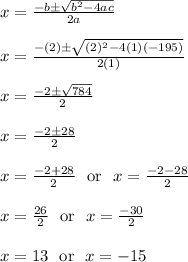
If x = 13, then x+2 = 13+2 = 15
Then note how x^2 + (x+2)^2 = 13^2 + 15^2 = 169 + 225 = 394
Or we could have x = -15 which leads to x+2 = -15+2 = -13
So, x^2 + (x+2)^2 = (-15)^2 + (-13)^2 = 225 + 169 = 394
We get the same thing either way.
Answer: Either 13, 15 or -15, -13