Answer:

Explanation:
There are three main trigonometric functions: sine, cosine, and tangent.
We are asked to find the cosine of angle P. The cosine is the ratio of the adjacent side to the hypotenuse.
In this triangle, the side measuring √7 is the adjacent side because it is next to angle P. The side measuring 10 is the hypotenuse because it is opposite the right angle.
- adjacent = √7
- hypotenuse= 10

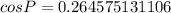
Round to the nearest hundredth. The 4 in the thousandths place to the right ( 0.264575131106) tells us to leave the 6 in the hundredths place.
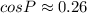
The cosine of angle P is approximately 0.26