Question

Felicia wants to build a kite with the shape shown. If AC is 60 cm, how many centimeters are in the length of BD?

Answer 1

Explanation:

By applying tangent rule in the given right triangle AOB,

tan(30°) =
`\frac{\text{Opposite side}}{\text{Adjacent side}}`

`(1)/(√(3))=(BO)/(OA)`

`OA=BO(√(3))`

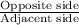
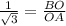
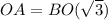
By applying tangent rule in the given right triangle BOC,

tan(60°) =
`(OC)/(BO)`

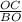
OC = BO(√3)

OA + OC = AC

`BO(√(3))+BO(√(3)) =60`

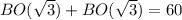
2√3(BO) = 60

BO = 10√3

OC = BO(√3)

OC = (10√3)(√3)

OC = 30

By applying tangent rule in right triangle DOC,

tan(60°) =
`(OD)/(OC)`

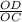
OD = OC(√3)

OD = 30√3

Since, BD = BO + OD

BD = 10√3 + 30√3

BD = 40√3

≈ 69.3