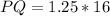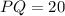Answer:
See explanation
Explanation:
Given
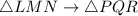
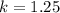
Required
The length of PQ
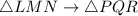 means that the side lengths of LMN are multiplied by 1.25 to get the side lengths of PQR
means that the side lengths of LMN are multiplied by 1.25 to get the side lengths of PQR
And it implies that the following sides are corresponding

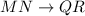

So, we have:
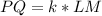
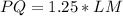
The question is incomplete.
Assume LM = 16, then: