Answer:
theta =
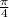 + 2
+ 2
 n,
n,
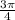 + 2
+ 2
 n,
n,
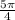 + 2
+ 2
 n,
n,
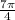 + 2
+ 2
 n
n
Explanation:
sin^2 theta - cos^3 theta = 1
cos^3 theta = 1 - sin^2 theta
sin^2 theta - cos^3 theta = 0
Substitute
sin^2 theta - ( 1 - sin^2 theta ) = 0
Distribute negative
sin^2 theta - 1 + sin^2 theta = 0
Combine same values
2sin^2 theta - 1 = 0
2sin^2 theta = 1
sin^2 theta =

sin theta = +-
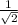
Right Triangle: 1 - 1 -

theta =
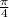 + 2
+ 2
 n,
n,
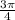 + 2
+ 2
 n,
n,
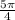 + 2
+ 2
 n,
n,
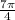 + 2
+ 2
 n
n
period of Sin function is 2
