Answer:
0.67 = 67% probability that a person who inquires about investments at this firm will invest in stocks or bonds (or both).
Explanation:
This question is solved treating these probabilities as Venn events.
I am going to say that:
Event A: Person invests in stocks.
Event B: Person invests in bonds.
65% of the people who inquire about investments at a certain brokerage firm end up investing in stocks
This means that
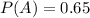
38% end up investing in bonds
This means that

36% end up investing in both stocks and bonds.
This means that
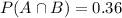
What is the probability that a person who inquires about investments at this firm will invest in stocks or bonds (or both)?
This is
 , given by the following equation:
, given by the following equation:
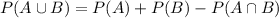
Considering the values we have for this problem:
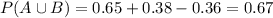
0.67 = 67% probability that a person who inquires about investments at this firm will invest in stocks or bonds (or both).