Answer:
(k) cos(θ)·√(1 + cot²θ) = √(cosec²θ - 1)
From trigonometric identities, we have;
1 + cot²θ = cosec²θ
On the Left Hand Side of the equation, we get;
cos(θ)·√(1 + cot²θ) = cos(θ) × cosec(θ) = cot(θ)
On the Right Hand Side of the equation, we have;
√(cosec²(θ) - 1) = √(1 + cot²(θ) - 1) = √(cot²(θ)) = cot(θ)
∴ √(cosec²θ - 1) = cot(θ)
By transitive property of equality, therefore;
cos(θ)·√(1 + cot²θ) = √(cosec²θ - 1)
(l) sin⁶A + cos⁶A = 1 - 3·sin²A·cos²A
sin⁶A + cos⁶A = (sin²A)³ + (cos²A)³
(sin²A)³ + (cos²A)³ = ((sin²A) + (cos²A))³ - 3·((sin²A)·(cos²A))·((sin²A) + (cos²A))
∴ (sin²A)³ + (cos²A)³ = (1)³ - 3·((sin²A)·(cos²A))·(1) = 1 - 3·((sin²A)·(cos²A))
sin⁶A + cos⁶A = (sin²A)³ + (cos²A)³ = 1 - 3·((sin²A)·(cos²A))
sin⁶A + cos⁶A = 1 - 3·((sin²A)·(cos²A))
(m) (sinA - cosecA)² + (cosA - secA)² = cot²A + tan²A - 1
(sinA - cosecA)² = sin²A - 2×sinA×cosecA + cosec²A = sin²A - 2 + cosec²A
(cosA - secA)² = cos²A - 2×cosA×secA + sec²A = cos²A - 2 + sec²A
∴ (sinA - cosecA)² + (cosA - secA)² = sin²A - 2 + cosec²A + cos²A - 2 + sec²A
Where;
sin²A - 2 + cosec²A + cos²A - 2 + sec²A = sin²A + cos²A - 2 - 2 + cosec²A + sec²A
sin²A + cos²A - 2 - 2 + cosec²A + sec²A = 1 - 4 + cosec²A + sec²A
1 - 4 + cosec²A + sec²A = cosec²A + sec²A - 3
Where;
cosec²A = cot²A + 1
sec²A = tan²A + 1
∴ cosec²A + sec²A - 3 = cot²A + 1 + tan²A + 1 - 3 = cot²A + tan²A - 1 = The Right Hand Side of the equation
∴ (sinA - cosecA)² + (cosA - secA)² = cot²A + tan²A - 1
(n)
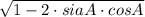 = sinA - cosA
= sinA - cosA
Squaring the Right Hand Side of the equation, we get;
(sinA - cosA)² = sin²A -2·sinA·cosA + cos²A = sin²A + cos²A -2·sinA·cosA
sin²A + cos²A -2·sinA·cosA = 1 - 2·sinA·cosA
∴ (sinA - cosA)² = 1 - 2·sinA·cosA
Taking the square root of both sides gives;
√((sinA - cosA)²) =
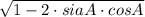
∴ sinA - cosA =
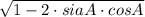
By symmetric property of equality, we have;
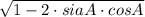 = sinA - cosA
= sinA - cosA
Explanation: