Answer:
Solution given:
Right angled triangle ABC is drawn where <C=
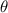
we know that
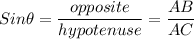
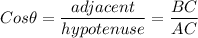
Now
left hand side
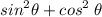
Substituting value
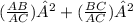
distributing power
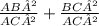
Taking L.C.M
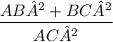 ....[I]
....[I]
In ∆ABC By using Pythagoras law we get
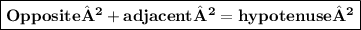
AB²+BC²=AC²
Substituting value of AB²+BC² in equation [I]
we get
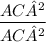
=1
Right hand side
proved