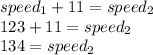Answer:
Slower trains: 123 km/h
Faster train: 134 km/h
Explanation:
In order to solve this problem, one must know the following formula:
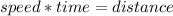
The problem gives one the following information:
- There are two trains heading towards each other, one is (11 km/h) faster than the other.
- There are (1542 km) between the two trains.
- It takes 6 hours for the two trains to meet each other.
Let (
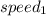 ) represent the speed of the slower train and (
) represent the speed of the slower train and (
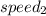 ) represent the speed of the faster train.
) represent the speed of the faster train.
One can form an equation, let (x) represent the speed of the slower train. Using the distance equation, one can state that the speed of each train times the travel time equals the distance. Since the trains met each other in (6) hours, and the combined distance traveled between the two trains is (1542 km); one can use this information to form an equation.
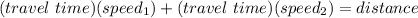
Substitute,
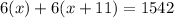
Simplify, distribute, multiply every term inside of the parenthesis by the term outside of it. Then combine like terms,
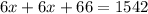
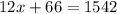
Inverse operations,
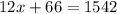
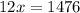
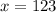
Solve for the speed of the faster train. It is given that it is (11 km/h) faster than the slower train.