Answer:

Step-by-step explanation:
Gravitational potential energy is the energy an object possesses due to its position. It is calculated using the following formula:
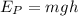
Where m is the mass, g is the acceleration due to gravity, and h is the height.
The object has a mass of 8.72 kilograms. Assuming this occurs on Earth, the acceleration due to gravity is 9.8 meters per second squared. The object gains 446 Joules of potential energy.
Let's convert the units of Joules. This makes the process of canceling units simpler later on. 1 Joule is equal to 1 kilogram meter squared per second squared. The object gains 446 J, which is equal to 446 kg *m²/s².
- EP= 446 kg*m²/s²
- m= 8.72 kg
- g= 9.8 m/s²
Substitute the values into the formula.
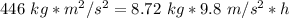
Multiply on the right side of the equation.
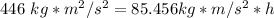
We are solving for the height, so we must isolate the variable h. It is being multiplied by 85.456 kg*m/s². The inverse operation of multiplication is division, so we divide both sides by this value.
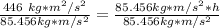
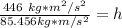
The units of kg*m/s² cancel, leaving meters as our unit.
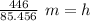
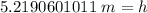
The original measurements of mass and potential energy have 3 significant figures, so our answer must have the same.
For the number we calculated, that is the hundredths place. The 9 in the thousandths place to the right tells us to round the 1 up to a 2.
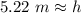
The object was lifted to a height of approximately 5.22 meters.