Answer: Choice B. (4, -1)
==========================================================
Step-by-step explanation:
Choice A can be ruled out because
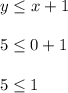
which is false.
Choices C and D are similar, so they can be ruled out as well.
---------------------
Choice B is the answer because it makes both inequalities true.
If we plug the coordinates of (4,-1) into the first inequality, we get
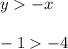
which is a true statement because -1 is to the right of -4 on the number line.
Now try the other inequality
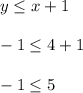
that's true also. So again, (4,-1) makes both inequalities true, and that's why choice B is the answer.