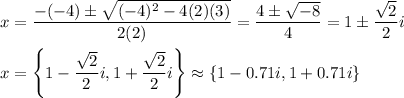9514 1404 393
Answer:
1a. -4, 3/4
1b. 1-0.71i, 1+0.71i
Explanation:
The directions tell you to use the quadratic formula. Factoring may get you the solution somewhat more easily, but does not comply with the directions.
The quadratic formula tells you ...
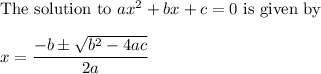
__
1a. a=4, b=13, c=-12
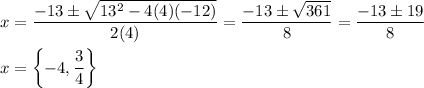
__
1b. After adding 3 to both sides, a=2, b=-4, c=3