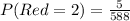Answer:
Dependent event
Explanation:
Given
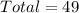
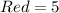
Solving (a): Are the events dependent?
Yes, they are.
When the first red candy is selected and eaten, the total number of candies reduced to 48 and the number of red candies also reduced to 4.
So, the probability of selecting a 2nd candy is dependent on the first candy selected.
Solving (b): P(Red = 2)
This is calculated as:
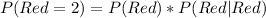
The first selection has the following probability:
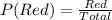
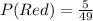
The second selection has the following probability:
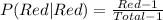
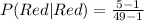
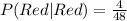
So, we have:
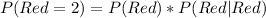
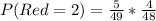
Reduce fraction
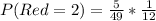
Multiply