Question

A simple pendulum consists of a ball of mass 3 kg hanging from a uniform string of mass 0.05 kg and length L. If the period of oscillation of the pendulum is 2 s, determine the speed of a transverse wave in the string when the pendulum hangs vertically.

Answer 1

v = 3.12 m/s

Step-by-step explanation:

First, we will find the length of the string by using the formula of the time period:

`T = 2\pi \sqrt{(l)/(g)}\\\\l = (T^2g)/(4\pi^2)\\\\`

where,

l = length of string = ?

T = time period = 2 s

g = acceleration due to gravity = 9.81 m/s²

Therefore,

`l = ((2\ s)^2(9.81\ m/s^2))/(4\pi^2)\\\\l = 0.99\ m`

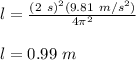
Now, we will find tension in the string in the vertical position through the weight of the ball:

T = W = mg = (3 kg)(9.81 m/s²)

T = 29.43 N

Now, the speed of the transverse wave is given as follows:

`v=\sqrt{(Tl)/(m)}\\\\v=\sqrt{((29.43\ N)(0.99\ m))/(3\ kg)}\\\\`

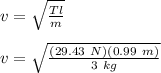
v = 3.12 m/s