Given:
The given equation is:
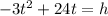
Where, t is the time in seconds and h is the height of the ball above the ground, measured in feet.
To find:
The inequality to model when the height of the ball is at least 36 feet above the ground. Then find time taken by ball to reach at or above 36 feet.
Solution:
We have,
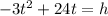
The height of the ball is at least 36 feet above the ground. It means
 .
.
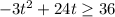
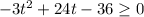
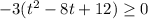
Splitting the middle term, we get
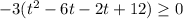
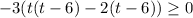
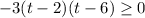
The critical points are:
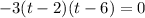
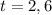
These two points divide the number line in 3 intervals
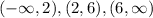 .
.
Intervals Check point
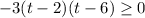 Result
Result
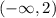 0
0
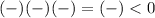 False
False
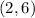 4
4
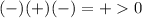 True
True
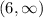 8
8
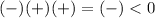 False
False
The inequality is true for (2,6) and the sign of inequality is
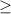 . So, the ball is above 36 feet between 2 to 6 seconds.
. So, the ball is above 36 feet between 2 to 6 seconds.
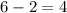
Therefore, the required inequality is
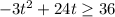 and the ball is 36 feet above for 4 seconds.
and the ball is 36 feet above for 4 seconds.