Answer:
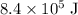 , assuming that there's no heat exchange between the washing machine and the environment.
, assuming that there's no heat exchange between the washing machine and the environment.
Step-by-step explanation:
Let
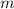 denote the mass of water and
denote the mass of water and
 the specific heat capacity of water. The energy required to raise the temperature of that much water by
the specific heat capacity of water. The energy required to raise the temperature of that much water by
 would be:
would be:
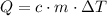 .
.
Washing at
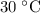 would require a temperature change of
would require a temperature change of
 .
.
Washing at
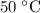 would require a temperature change of
would require a temperature change of
 .
.
In both situations,
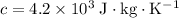 while
while
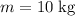 .
.
Calculate the energy required in either situation:
Washing at
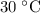 :
:
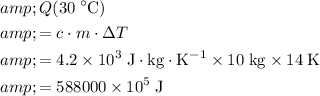 .
.
Washing at
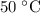 :
:
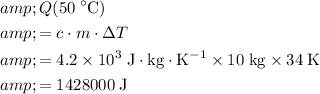 .
.
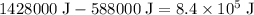 .
.