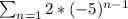Question

Write the sum using summation notation, assuming the suggested pattern continues.

2, -10, 50, -250, +…

Is this sequence arithmetic or geometric? How do you know?

Answer 1

`\sum_(n = 1) 2*(-5)^(n-1)`

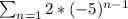
Explanation:

An arithmetic sequence is of the form:

`A_n = A_(n-1) + d`

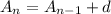
While a geometric sequence is of the form:

`A_n = A_(n-1)*r`

notice that first, we have a change of sign in our sequence, so we already can discard the arithmetic sequence.

In fact, the pattern is kinda easy to see.

The first term is:

A₁ = 2

the second term is:

A₂ = -10

notice that:

A₂/A₍ = r = -10/2 = -5

The third term is:

A₃ = 50

the quotient between the third term and the second term is:

A₃/A₂ = 50/-10 = -5

Whit this we can already conclude that the n-th term of our sequence will be:

`A_n = A_(n-1)*(-5)`

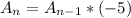
Then the summation will be something like:

`\sum_(n = 1) A_n = A_1 + A_2 + A_3 + ... = 2 - 10 + 50 - ...`

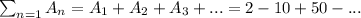
We can write:

`A_n = A_(n-1)*(-5) = (A_(n-2)*(-5))*(-5)) = A_1*(-5)^(n-1) = 2*(-5)^(n-1)`

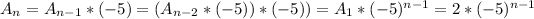
Then the summation is just:

`\sum_(n = 1) 2*(-5)^(n-1)`