Recall that if |x| < 1, then
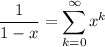
So if |a + bxᵐ| < 1, then
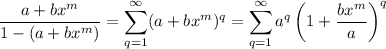
By the binomial theorem,
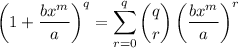
The binomial coefficient is defined as
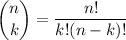
if 0 ≤ k ≤ n, and 0 otherwise. Then we can rewrite the sum as
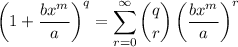
and pulling out the first term,
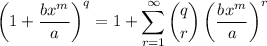
Finally,
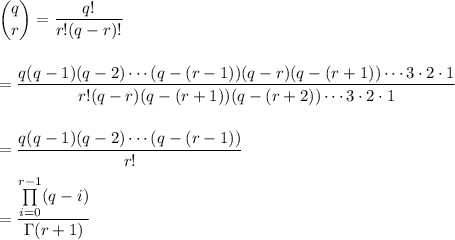
since n! = Γ(n + 1). (I think the given upper limit in the product may be a mistake.)