Answer: 100 tickets.
Explanation:
- Number of $8 tickets sold = x
- Number of $12 tickets sold = y
Set up two equations: one representing total amount sold and another representing total dollars earned.
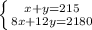
Rearrange x + y = 215 and find the value of x:
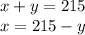
Substitute it into the other equation and solve for y:
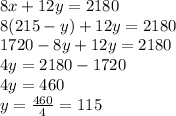
Substitute in the y-value to the other expression to find x:
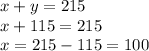
Therefore, they sold 100 of the $8 tickets.