Question

A 77 turn, 10.0 cm diameter coil rotates at an angular velocity of 8.00 rad/s in a 1.18 T field, starting with the normal of the plane of the coil perpendicular to the field. Assume that the positive max emf is reached first.

a. What is the peak emf?
b. At what time is the peak emf first reached?
c. At what time is the emf first at its most negative?
d. What is the period of the AC voltage output?

Answer 1

a) fem = 5.709 V, b) t = 0.196 s, c) t = 0.589 s, d) T = 0.785 s

Step-by-step explanation:

This is an exercise in Faraday's law

fem= - N
`(d \Phi _B)/(dt)`

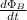
fem = - N
`(d \ (B A cos \theta))/(dt)`

The magnetic field and the area are constant

fem = - N B A
`(d \ cos \ \theta)/(dt)`

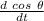
fem = - N B A (-sin θ)
`(d \theta)/(dt)`

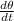
fem = N B (π d² / 4) sin θ w

fem=
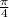`(\pi )/(4)` N B d² w sin θ

with this expression we can correspond the questions

a) the peak of the electromotive force

this hen the sine of the angle is 1

sin θ = 1

fem =
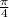`(\pi )/(4)` 77 1.18 0.10² 8.0

fem = 5.709 V

b) as the system has a constant angular velocity, we can use the angular kinematics relations

θ = w₀ t

t = θ/w₀

Recall that the angles are in radians, so the angle for the maximum of the sine is

θ= π/2

t =
`(\pi )/(2) \ (1)/(8)`

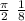
t = 0.196 s

c) for the electromotive force to be negative, the sine function of being

sin θ= -1

whereby

θ = 3π/ 2

t =
`(3\pi )/(2) \ (1)/(8)`

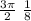
t = 0.589 s

d) This electromotive force has values ​​that change sinusoidally with an angular velocity of

w = 8 rad / s

angular velocity and period are related

w = 2π / T

T = 2π / w

T = 2π / 8

T = 0.785 s