Question

A gas at 100 Celsius has a volume of 33.5 L. What is its new volume after it is cooled to 25 Celsius?

Answer 1

`\boxed {\boxed {\sf 8.38 \ L}}`

Step-by-step explanation:

We are asked to find the new volume of a gas after a change in temperature. We will use Charles's Law, which states the volume of a gas is directly proportional to the temperature. The formula for this law is:

`\frac {V_1}{T_1}= (V_2)/(T_2)`

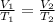
The gas starts at 100 degrees Celsius and a volume of 33.5 liters. Substitute these values into the formula.

`\frac {33.5 \ L}{100 \textdegree C}=( V_2)/(T_2)`

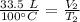
The gas is cooled to 25 degrees Celsius, but the volume is unknown.

`\frac {33.5 \ L}{100 \textdegree C}=( V_2)/(25 \textdegree C)`

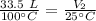
We want to find the volume of the gas after it is cooled. We must isolate the variable V₂. It is being divided by 25 degrees Celsius and the inverse of division is multiplication. Multiply both sides of the equation by 25 °C.

`25 \textdegree C*\frac {33.5 \ L}{100 \textdegree C}=( V_2)/(25 \textdegree C)* 25 \textdegree C`

`25 \textdegree C*\frac {33.5 \ L}{100 \textdegree C}= V_2`

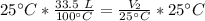
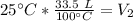
The units of degrees Celsius cancel.

`25*\frac {33.5 \ L}{100 }= V_2`

`8.375 \ L = V_2`

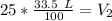
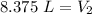
The original measurements have 3 significant figures, so our answer must have the same. For the number we found, that is the hundredth place. The 5 in the thousandths place tells us to round the 7 up to an 8.

`8.38 \ L \approx V_2`

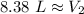
The new volume after the gas is cooled is approximately 8.38 liters.