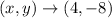Answer:
(a)
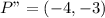
(b)
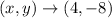
Explanation:
Given
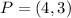
Solving (a): Reflect across x and y-axis.
Reflection across x-axis has the following rules
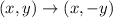
So, we have:
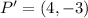
Reflection across y-axis has the following rules
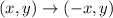
So, we have:
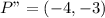
Hence, the new point is: (-4,-3)
Solving (b): Rx . Do,2 (2,4)
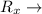 reflect across the x-axis
reflect across the x-axis
Reflection across x-axis has the following rules
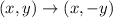
So, we have:
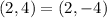 ---- when P is reflected across the x-axis
---- when P is reflected across the x-axis
 dilate by a scale factor of 2
dilate by a scale factor of 2
The rule is:
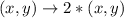
So, we have
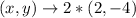
Open bracket