Answer:
0.2222 = 22.22% probability of earning exactly 5 points.
Explanation:
A probability is the number of desired outcomes divided by the number of total outcomes.
Possible outcomes:
For the pair of dice:
(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)
So 36 total outcomes.
If the sum is between 6 and 9, inclusive, the amount of points awarded is the sum minus 3.
Sum of 8 -> 5 points awarded. So
(2,6), (3,5), (4,4), (5,3), (6,2): 5 outcomes.
If the sum is between 10 and 12, inclusive, the amount of points awarded is the sum minus 5.
Sum of 10 -> 5 points awarded. So
(4,6), (5,5), (6,4): 3 outcomes.
Desired outcomes:
5 + 3 = 8
Calculate the probability of earning exactly 5 points.
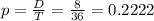
0.2222 = 22.22% probability of earning exactly 5 points.