Question

A smokestack of height H = 50 m emits a pollutant in a 3 m/s wind. The plume is carried downwind by advection (wind speed U = 3 m/s) and is simultaneously dispersing vertically with a turbulent diffusion coefficient D. The vertical diffusion causes the plume to widen vertically over time, with halfâwidth (distance from centerline to edge) increasing as:

half width = 2 â2Dt

The plume reaches the ground some distance L downwind of the base of the smokestack (see sketch in book on page 203)

a. If L = 2 km, estimate the value of the turbulent diffusion coefficient D.
b. Under the same wind speed and turbulence conditions, what would be the value of L if the smokestack were twice as high?

Answer 1

a) 0.46875

b) 8 km

Step-by-step explanation:

Smokestack height ( H ) = 50 m

speed of pollutant / wind speed = 3 m/s

Half width = 2
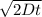`√(2Dt )` = 50 m ---- ( 1 )

a) If L = 2 km

value of turbulent diffusion coefficient D

back to equation 1

50 = 2 √ 2 * D * ( 2000/3 )

2500 = 4 * 2 * D * ( 2000/3 )

D = 2500 / ( 8 * ( 2000/3 ) )

= 0.46875

where : time to travel ( t ) = Distance / speed = 2000 / 3

b) when the smoke stack = 50 * 2 = 100 m

L = 800 m = 8 km

attached below is the detailed solution