Part (a)
The standard error (SE) formula is
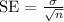
where n is the sample size. We're given SE = 2 and sigma = 34, so,
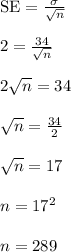
So we need a sample size of n = 289 to have an SE value of 2.
Answer: 289
========================================================
Part (b)
We'll use SE = 1 this time
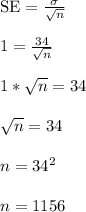
Because we require greater precision (i.e. a smaller SE value), the sample size must be larger to account for this. In other words, as SE goes down, then n must go up, and vice versa.
Answer: 1156