Question

The world’s tallest building is the Burj Khalifa which stands at 828 m above the ground. An eccentric billionaire CEO has an office on the top floor. He insists on having a personal elevator installed that consists only of a giant spring that spans from the basement to his office when it is uncompressed. If his mass is 120 kg, what spring constant in N/m is required so that he momentarily comes to rest on the ground floor?

Answer 1

The spring constant is approximately 2.84 N/m

Step-by-step explanation:

The height of the building, h = 828 m

The mass of the billionaire that has an office on the top floor, m = 120 kg

Gravitational potential energy, P.E. = m·g·h

Where;

g = The acceleration due to gravity ≈ 9.81 m/s²

The gravitational potential energy of the billionaire at the top floor is therefore;

P.E. of billionaire at top floor = 120 kg × 9.81 m/s² × 828 m = 974,721.6 J

The elastic potential energy of the spring,
`P.E._(spring)` is given as follows;

`P.E._(spring) = (1)/(2) \cdot k \cdot h^2`

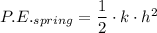
Where;

k = The spring constant of the spring in N/m

h = The extension of the spring = The height of the building = 828 m

Given that the energy of the spring is conserved, we have;

`P.E._(spring)` = P.E. of billionaire = 974,721.6 J

Plugging in the values gives;

`P.E._(spring) = 974,721.6 \ J = (1)/(2) * k * (828 \ m)^2`

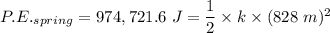
Therefore;

2*974,721.6/(828^2)

`k = (2 * 974,721.6 \ J)/((828 \ m)^2) \approx 2.84 \ N/m`

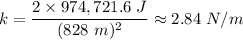
The spring constant, k ≈ 2.84 N/m.