Answer:
Center: (1,3)
Radius: 6
Explanation:
Hi there!
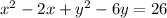
Typically, the equation of a circle would be in the form
 where
where
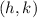 is the center and
is the center and
 is the radius.
is the radius.
To get the given equation
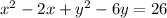 into this form, we must complete the square for both x and y.
into this form, we must complete the square for both x and y.
1) Complete the square for x
Let's take a look at this part of the equation:
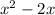
To complete the square, we must add to the expression the square of half of 2. That would be 1² = 1:
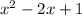
Great! Now, let's add this to our original equation:
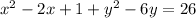
We cannot randomly add a 1 to just one side, so we must do the same to the right side of the equation:

Complete the square:
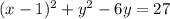
2) Complete the square for y
Let's take a look at this part of the equation
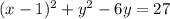 :
:
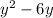
To complete the square, we must add to the expression the square of half of 6. That would be 3² = 9:

Great! Now, back to our original equation:
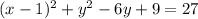
Remember to add 9 on the other side as well:
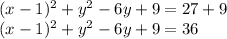
Complete the square:

3) Determine the center and the radius


Now, we can see that (1,3) is in the place of (h,k). 36 is also in the place of r², making 6 the radius.
I hope this helps!