Answer:
Imaginary roots
Explanation:
The discriminant of a quadratic in standard form
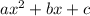 is given by
is given by
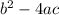 .
.
Given
 , subtract 5x from both sides so that the quadratic is in standard form:
, subtract 5x from both sides so that the quadratic is in standard form:
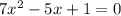
Now assign variables:
The discriminant is therefore
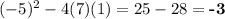 .
.
What does this tell us about the roots?
Recall that the discriminant is what is under the radical in the quadratic formula. The quadratic formula is used to find the solutions of a quadratic. Therefore, the solutions of this quadratic would be equal to
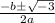 for some
for some
 and
and
 . Since the number under the radical is negative, there are no real roots to the quadratic (whenever the discriminant is negative, the are zero real solutions to the quadratic). Therefore, the quadratic has imaginary roots.
. Since the number under the radical is negative, there are no real roots to the quadratic (whenever the discriminant is negative, the are zero real solutions to the quadratic). Therefore, the quadratic has imaginary roots.